A Nonlinear Eigenvalue Problem

eigen mesh0

In this problem, we solve the nonlinear eigenvalue problem -Laplace u= \lambda sin(u) on the unit square with Dirichlet boundary conditions. The problem is solved using the continuation options in PLTMG. The continuation is carried out on a uniform coarse mesh.

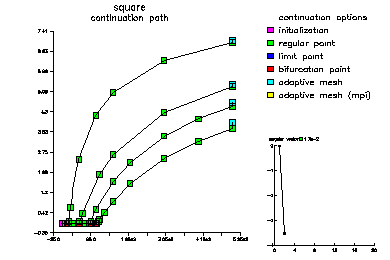
eigen path

We compute the first four eigenfuctions. Here is a picture of the continuation path. At the points colored cyan the mesh is adaptively refined and a more accurate approximation is computed.

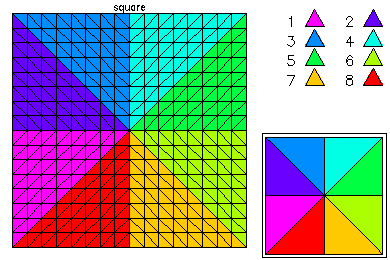
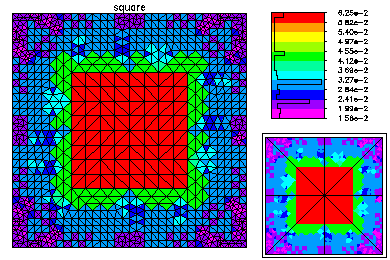
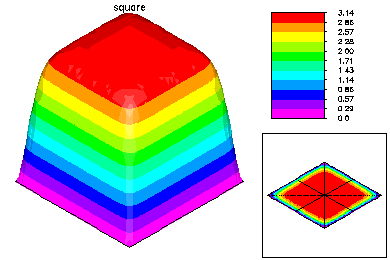
eigen mesh1 eigen soln1

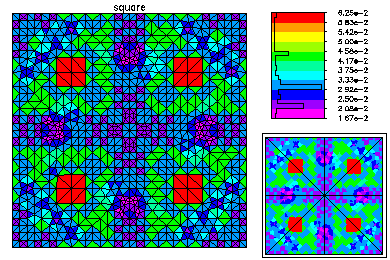
Here is the refined mesh and the first eigenfunction. The refined mesh is colored by element size.

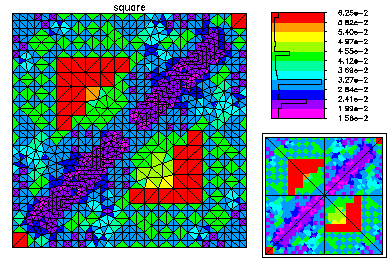
eigen mesh2 eigen soln2

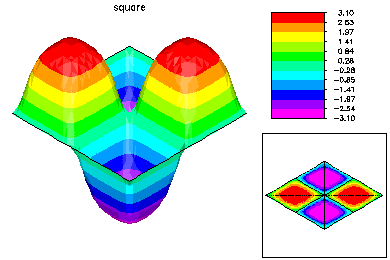
Here is the refined mesh and the second eigenfunction. The second eigenvalue has multiplicity two, but only a single (arbitrary) eigenfuction is computed.

eigen mesh3 eigen soln3

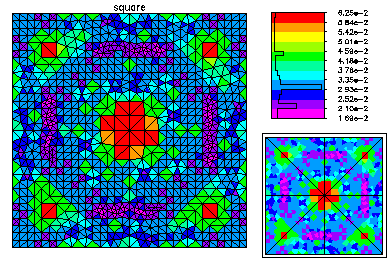
Here is the refined mesh and the third eigenfunction.

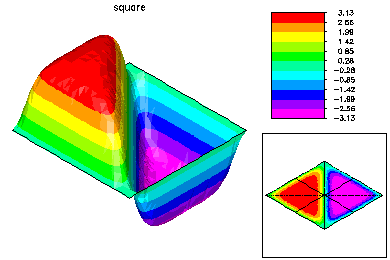
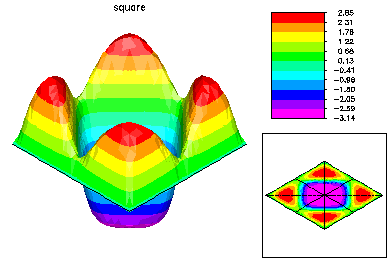
eigen mesh4 eigen soln4

Here is the refined mesh and the fourth eigenfunction. The fourth eigenvalue also has multiplicity two.